Hexadecimal Number System
The Decimal number system (base-10) consists of the following digits:
0 1 2 3 4 5 6 7 8 9
The Binary number system (base-2) consists of the following digits:
0 1
Most humans use decimal and computers use binary. As computer scientists, it's helpful to express data as the computer does. The problem is that large strings of 0s and 1s can be difficult to understand.
For example, something like this ‘0100100010100101010100100100’ is not immediately obvious. But we still need to be able to express data as a computer does. Therefore, we have this notion of hexadecimal.
What is Hexadecimal?
The Hexadecimal number system (base-16) consists of the following digits:
0 1 2 3 4 5 6 7 8 9 A B C D E F
Hexadecimal is a much more concise way of expressing binary information on a computer system. It is much more human-readable.
Why Base-16?
16 is a power of 2 (2⁴ = 16). This means each hexadecimal digit can correspond to a unique arrangement of a 4-bit binary 0000 (4-digit).
Note that a 4-bit binary 0000 is also known as a Nibble
Therefore, we can represent really long chains of binary as hexadecimal without cumbersome conversions.
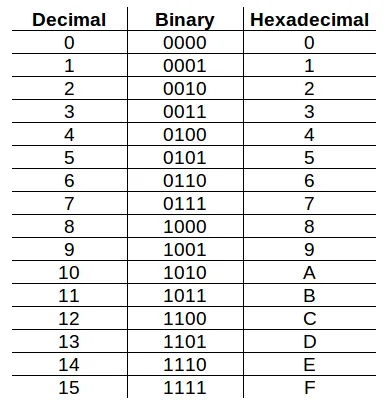
Figure 1: Converting binary 1001 1110 0101 0011 to hexadecimal 0x9E53
For example, the binary number: 10011110
Can be split into two 4-bit pieces: 1001 1110 and each of these can be converted to hexadecimal: 1001 1110 => 9E
How tidy!
Hexadecimal Notation
But 9E just looks like any other decimal number 9 followed by an E. Or someone may misinterpret it as being 9*E. How do we specify that we are talking about hexadecimal numbers?
You can simply prefix a hexadecimal number with 0x. That means that 9E can be written as 0x9E. This way anyone would be able to tell if this is hexadecimal or not.
Note that 0× has no meaning.
So you can write it as:
0x0 0x1 0x2 0x3 0x4 0x5 0x6 0x7 0x8 0x9 0xA 0xB 0xC 0xD 0xE 0xF
Converting Binary to Hexadecimal
So, for example, a binary:
0100 0110 1010 0010 1011 1001 0011 1101
Can be split into 4 digits and be converted in hexadecimal as follows:
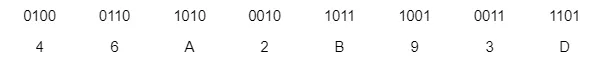
Final answer = 0x46A2B93D
Conclusion
The skill of working with hexadecimal numbers is valuable for computer scientists. While it may not involve complex mathematical operations, it plays a crucial role in computer science and programming. For example, a lot of the time memory addresses are represented as hexadecimal and so on.